Análise de Impedância, Impedância de Entrada e Impedância de Saída

Impedância é um termo coletivo para resistência e reatância, e a maior diferença entre resistência e reatância é que a limitação de corrente de resistência (lei de Ohm) consome energia elétrica ao mesmo tempo. A reatância é limitada à corrente e não consome energia elétrica (sem realizar trabalho). A resistência tem um efeito de corrente limitado tanto em corrente contínua como em corrente alternada, enquanto a reatância só tem um efeito de corrente limitado em ambientes de corrente alternada.

A impedância de entrada refere-se à impedância equivalente na extremidade de entrada de um circuito. Adicione uma fonte de tensão U ao terminal de entrada e meça a corrente I no terminal de entrada, então a impedância de entrada Rin é U/I. Você pode imaginar a extremidade de entrada como as duas extremidades de um resistor, e o valor da resistência desse resistor é a impedância de entrada.

Sob a mesma tensão de entrada, se a impedância de entrada for muito baixa, uma grande corrente precisa fluir, o que testa a capacidade de saída de corrente do estágio anterior; Se a impedância de entrada for alta, apenas uma pequena quantidade de corrente será necessária, o que reduz uma carga significativa na capacidade de saída de corrente do estágio frontal. Portanto, no projeto do circuito, tente aumentar a impedância de entrada tanto quanto possível.

A impedância de entrada não é diferente de um componente de reatância comum, pois reflete a magnitude do efeito de bloqueio da corrente.

Para circuitos acionados por tensão, quanto maior a impedância de entrada, mais leve será a carga na fonte de tensão, facilitando o acionamento sem afetar a fonte do sinal; Para circuitos acionados por corrente, quanto menor for a impedância de entrada, mais leve será a carga na fonte de corrente.

Portanto, podemos pensar que se uma fonte de tensão for usada para acionar, quanto maior a impedância de entrada, melhor; Se for acionado por uma fonte de corrente, quanto menor a impedância, melhor (nota: adequado apenas para circuitos de baixa frequência, em circuitos de alta frequência, o casamento de impedância também deve ser considerado). a correspondência também deve ser considerada.Impedância de saída

A impedância de saída inclui a impedância interna da fonte de tensão equivalente (circuito equivalente de Thevenin) ou fonte de corrente equivalente (circuito equivalente de Norton) da porta de saída da rede de energia independente. Seu valor é igual à impedância de entrada vista na porta de saída quando a fonte de alimentação independente é zerada.

Independentemente da fonte do sinal, amplificador e fonte de alimentação, há um problema com a impedância de saída. A impedância de saída é a resistência interna de uma fonte de sinal. Originalmente, para uma fonte de tensão ideal (incluindo fonte de alimentação), a resistência interna deveria ser 0, ou a impedância de uma fonte de corrente ideal deveria ser infinita. A impedância de saída precisa de atenção especial no projeto do circuito.

Na realidade, as fontes de tensão não conseguem isso, e uma fonte de tensão ideal é frequentemente conectada em série com um resistor r para equivaler a uma fonte de tensão real. O resistor r em série com a fonte de tensão ideal é a resistência interna da fonte de sinal/saída do amplificador/fonte de alimentação.

Quando esta fonte de tensão fornece energia à carga, uma corrente I fluirá através da carga e gerará I neste resistor × A queda de tensão de r. Isto resultará em uma diminuição na tensão de saída da fonte de alimentação, limitando assim a potência máxima de saída.

Da mesma forma, uma fonte de corrente ideal deveria ter uma impedância de saída infinita, mas circuitos reais são impossíveis.

A impedância de saída refere-se à impedância equivalente do circuito quando a carga do circuito é vista da porta de saída do circuito na direção oposta. Na verdade, refere-se principalmente à impedância medida pela fonte de energia na extremidade de saída, comumente conhecida como resistência interna.

Análise de pensamento de impedância de circuitos de comutação

Conforme mostrado na figura a seguir, V1 continua a fornecer corrente para R1, e o circuito de corrente na figura é mostrado pela seta verde. Que métodos temos se quisermos controlar o fluxo de corrente para R1?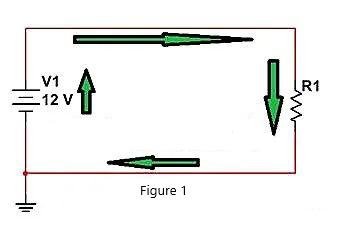

O método mais comum é desconectar a conexão entre V1 e R1 e cortar o circuito de corrente. Conforme mostrado na figura a seguir.

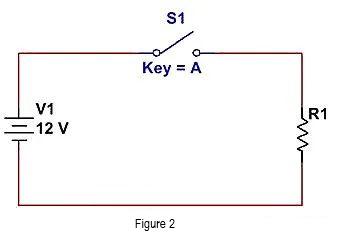
Alternativamente, podemos ignorar R1 conforme mostrado na figura a seguir. Adicione um fio na frente de R1 para direcionar a corrente para o caminho com baixa impedância, e R1 obterá uma corrente insignificante.

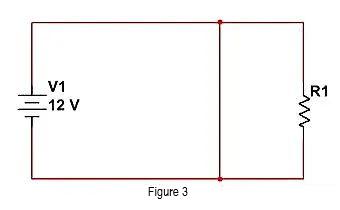
Os dois métodos acima são muito simples, desconectando completamente o caminho de V1 a R1 ou curto-circuitando R1, o que resolve o problema completamente. Mas no mundo da engenharia, não podemos fazê-lo de forma tão limpa e ordenada, muitas vezes enfatizando uma solução “semelhante”. abordagem. Assim, no "modelo de curto-circuito", só podemos alcançar "baixa impedância", enquanto no "modelo de circuito aberto", só podemos alcançar "alta impedância". Se a energia for significativamente "atenuada", acreditamos que ela atende ao padrão.

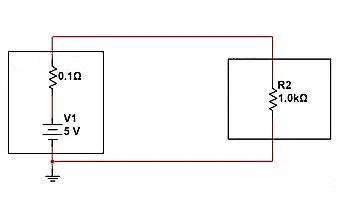
Conforme mostrado na figura abaixo, o modelo real de carga de energia é mostrado. Vamos ver como conseguir o efeito de comutação ajustando a impedância. Em circuitos reais, as fontes de energia têm limitações de capacidade de saída e resistência interna, e quanto maior a corrente de saída, menor será a tensão de saída.

O circuito a seguir tem uma resistência interna de 0,1 Ω e uma carga de 1K Ω. Na situação atual, a tensão obtida em ambas as extremidades da carga é composta por resistência interna e tensão parcial R2. Podemos calcular V=5V * (1K/(1K+0,1))=4,9999V, I=5V/1000,1 Ω=4,9mA.

Se usarmos o "modelo de circuito aberto" método para interromper o circuito, como devemos ajustar a impedância? Consiste em conectar um resistor muito maior que 1K em série entre a fonte de alimentação e a carga, e realizar a divisão da tensão em série para reduzir a tensão obtida em R2. Conforme mostrado na figura a seguir, se um resistor de 1M estiver conectado em série com o divisor de tensão de carga. Podemos calcular a distribuição final de tensão entre as duas extremidades da carga:

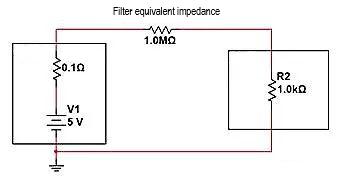
V=5V * (1K/(0,1+1000K+1K))=0,00499V, I=5V/1001000,1 Ω=0,0049mA. A amplitude foi enfraquecida quase 1000 vezes e, no pensamento da engenharia, R2 está quase “desconectado”.

Se usarmos o "modelo de curto-circuito" método para desconectar R2, como devemos ajustá-lo? Consiste em conectar um resistor bem menor que 0,1 Ω em paralelo na extremidade frontal da carga e realizar o compartilhamento de tensão em série com o resistor interno, resultando em uma tensão menor obtida em R2.

Conforme mostrado na figura a seguir, se a medida de filtragem for equivalente a um resistor paralelo de 0,005 Ω e um divisor de tensão de resistência interna. Podemos calcular a tensão final distribuída entre as duas extremidades da carga R2:

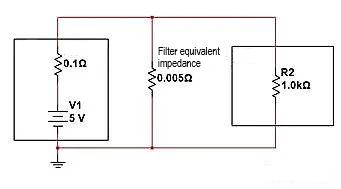
V=5V * (0,0049/(0,1+0,0049)=0,233V. A amplitude foi enfraquecida quase 20 vezes e, no pensamento de engenharia, R2 também é semelhante a estar "desconectado".

O acima é o modelo teórico de circuitos de chave semicondutores, tomando como exemplo os circuitos inversores:

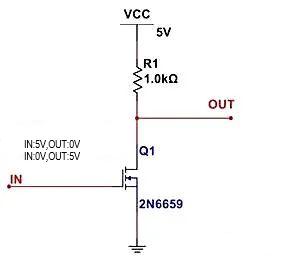
Quando a extremidade IN estiver energizada, diremos que o transistor MOS Q1 está conduzindo. Neste ponto, o estado de condução é equivalente a Q1 se tornar um resistor com impedância de dezenas de miliohms e então dividir a tensão com o resistor R1. Se o resistor pull-up R1 for muito pequeno e também dezenas de miliohms, mesmo que IN seja alto e Q1 esteja conduzindo, o terminal OUT não poderá produzir um nível baixo.

Quando a extremidade IN for desligada, diremos que o transistor MOS Q1 está desligado. Neste ponto, o estado de corte é equivalente a Q1 se tornar um resistor com impedância de alguns megaohms e dividir a tensão com o resistor R1. Se o resistor pull-up R1 for muito grande, que também é de alguns megaohms, mesmo que IN esteja baixo e Q1 esteja cortado, o terminal OUT não poderá produzir um nível alto.

Portanto, ao compreender profundamente os circuitos de comutação, é necessário analisá-los com pensamento de impedância.

Circuito de filtro de análise de pensamento de impedância

Aqui, analise o circuito de filtragem usando o pensamento de impedância.

Em aplicações práticas de engenharia, uma saída de energia geralmente contém componentes CA de frequências diferentes, tanto o que queremos quanto o que não queremos. A impedância da indutância e da capacitância variará com a frequência. É precisamente por causa dessa característica que indutores e capacitores se tornaram os principais atores nos circuitos de filtragem.

O circuito a seguir ainda é usado, assumindo que a fonte de alimentação contém um componente espectral de
0-1 GHz.

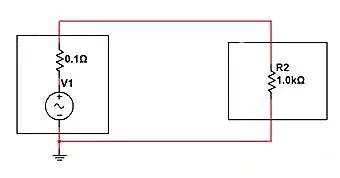
Se quisermos filtrar componentes CA de alta frequência para a carga R2, descobriremos que tanto a indutância em série quanto a capacitância paralela podem atender aos requisitos.
Conforme mostrado na figura a seguir, se um indutor de 16uH for conectado em série entre a fonte de alimentação e a carga, quanto o componente CA de 100 MHz diminuirá? De acordo com a fórmula de impedância da indutância: ZL=2 π fL=2 * 3,14 * 100MHz * 16uH, ZL=10K pode ser obtido.

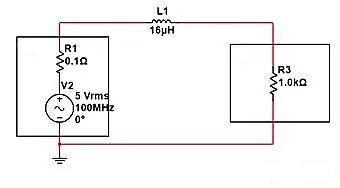
De acordo com a fórmula do divisor de tensão em série, a tensão/entrada em ambas as extremidades de R3=R3/(R3+ZL)=1K/11K=0,0909. Portanto, quando a amplitude da fonte de alimentação é 5V, a amplitude em ambas as extremidades de R3 é de apenas 5V * 0,0909=0,45V.

A 100 MHz, use um osciloscópio para medir a forma de onda antes e depois da filtragem. A comparação mostra que a forma de onda de 100 MHz tem efeito e a medição real é de 0,449 V, o que é consistente com os resultados da análise.

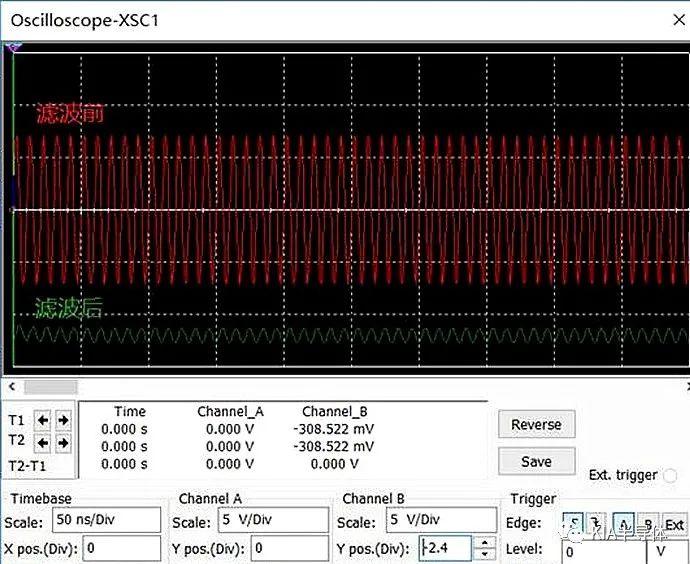
Análise de pensamento de impedância de filtros passa-baixa

Ao conectar um indutor em série entre a fonte de alimentação e a carga e conectar um capacitor em paralelo na extremidade frontal da carga, um circuito de filtro passa-baixa é formado.

Como segue, se C1=1uF e L1=22uH, qual é o grau de atenuação do circuito de filtragem para o
Componente CA de 100 MHz?

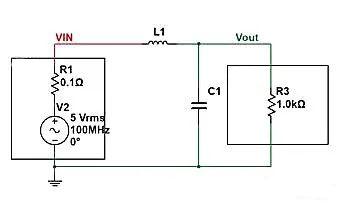
Neste ponto, o circuito é conectado em paralelo com a impedância Zc do capacitor (C1) e R3, e depois dividido com a impedância ZL do indutor (L1). Portanto, podemos listar a equação de impedância (que é uma fórmula simples de divisor de tensão em série).

Amplitude de atenuação=Vout/Vin=(Zc//R3)/(ZL+(Zc/R3)

Entre eles, Zc=1/2 π fC e ZL=2 π fL. Dado R3=1K Ω, pode-se concluir que Zc=0,0015 Ω, Zc/R=0,00149 Ω.

ZL=13816 Ω, a amplitude de atenuação pode ser obtida como 0,00149/(13816,00149)=0,000000178.

Pode-se observar que o componente CA de 100 MHz dificilmente consegue passar pelo circuito de filtragem passa-baixa de 22uH e 1uF. Ao mesmo tempo, vemos também que a carga R3 pode afetar o efeito de filtragem do filtro. Portanto, às vezes descobrimos que o mesmo circuito de filtro funciona bem neste circuito, mas mal em outros circuitos.